Cunningham Chains (1st kind)
The Prime Pages keeps a list of the 5000 largest
known primes, plus a few each of certain selected archivable forms and
classes. These forms are defined in this collection's home page.
This page is about one of those forms.
Definitions and Notes
Recall that a
Sophie Germain prime is a
prime p such that
q=2
p+1 is also prime. Why not also ask that
r=2
q+1 is prime,
and 2
r+1 is prime, and...? A
Cunningham chain of
length k of the first kind is a
sequence of
k primes, each which is twice the proceeding one plus one. For example, {2, 5, 11, 23, 47} and {89, 179, 359, 719, 1439, 2879}. This means the terms in such a sequence are
p, 2
p+1, 4
p+3, 8
p+7, ... so if a prime is labelled "(4
p+3)" in the table of primes, it is the third term in a sequence of (at least) three primes.
We have a separate page about the Cunninham chains of the second kind and the Sophie Germain primes.
Cunningham chains (of both kinds) are also called chains of nearly doubled primes.
For any given length k there should be infinitely
many chains of length k. In fact the number less than
N should be asymptotic to
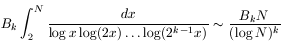
where
where the sequence
Bk begins approximately 1.32032 (
k=2), 2.85825, 5.553491, 20.2636, 71.9622, 233.878, 677.356.
Because the Sophie Germain primes have their own
Top Twenty page, they are not included in the list of records below. Forthe same reason
'Cunningham Chain (p)'s and 'Cunningham Chain (2p+1)'s (which are Sophie Germain primes) are omitted.
Record Primes of this Type
Cunningham chain (4p+3)
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 1128330746865 · 266441 - 1 |
20013 |
p158 |
Feb 2020 |
Cunningham chain (4p + 3) |
| 2 | 1815615642825 · 244046 - 1 |
13272 |
p395 |
Nov 2016 |
Cunningham chain (4p + 3) |
| 3 | 778965587811 · 236627 - 1 |
11038 |
p395 |
Sep 2016 |
Cunningham chain (4p + 3) |
| 4 | 272879344275 · 236622 - 1 |
11036 |
p395 |
Aug 2016 |
Cunningham chain (4p + 3) |
| 5 | 333645655005 · 235549 - 1 |
10713 |
p364 |
Mar 2015 |
Cunningham chain (4p + 3) |
|
Cunningham chain (8p+7)
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 744029027072 · 10111# - 1 |
4362 |
p364 |
Feb 2025 |
Cunningham chain (8p + 7) |
| 2 | 1268118079424 · 8501# - 1 |
3640 |
p434 |
Oct 2023 |
Cunningham chain (8p + 7) |
| 3 | 109766820328 · 7877# - 1 |
3385 |
p395 |
Nov 2016 |
Cunningham chain (8p + 7) |
| 4 | 231692481512 · 7517# - 1 |
3218 |
p395 |
Sep 2016 |
Cunningham chain (8p + 7) |
| 5 | 375967981369 · 6907# · 8 - 1 |
2972 |
p382 |
May 2017 |
Cunningham chain (8p + 7) |
|
Cunningham chain (16p+15)
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 7610828704751636272 · 4679# - 1 |
2020 |
p151 |
Feb 2024 |
Cunningham chain (16p + 15) |
| 2 | 54201838768 · 3917# - 1 |
1681 |
p395 |
Oct 2016 |
Cunningham chain (16p + 15) |
| 3 | 3199190962192 · 3499# - 1 |
1494 |
p382 |
Mar 2016 |
Cunningham chain (16p + 15) |
| 4 | 5780736564512 · 3023# - 1 |
1301 |
p364 |
Mar 2015 |
Cunningham chain (16p + 15) |
| 5 | 1542946580224 · 2851# - 1 |
1231 |
p364 |
Aug 2023 |
Cunningham chain (16p + 15) |
|
Cunningham chain (32p+31)
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 89595955370432 · 2371# - 1 |
1017 |
p364 |
Mar 2015 |
Cunningham chain (32p + 31) |
|
Weighted Record Primes of this Type
For amusement purposes only we might seek to weight the
chains on the list of largest known primes by an estimate
of how rare chains of that length are. We also include
the Sophie Germain primes because they are chains of
length two.
To form a weight we start with the
usual estimate of how hard it is to prove primality of a
number the size of n
log(n)2 log log n
and multiply it by the expected number of potential candidates
to test before we find one of length
k (by the heuristic estimate above)
log(n)k / Bk.
We then take the log one more time to make the numbers nice
and small.
(Because the Sophie germain primes have their own
Top Twenty page, they are not included in the list of records below.)
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 89595955370432 · 2371# - 1 |
1017 |
p364 |
Mar 2015 |
Cunningham chain (32p + 31) |
| 2 | 7610828704751636272 · 4679# - 1 |
2020 |
p151 |
Feb 2024 |
Cunningham chain (16p + 15) |
| 3 | 54201838768 · 3917# - 1 |
1681 |
p395 |
Oct 2016 |
Cunningham chain (16p + 15) |
| 4 | 3199190962192 · 3499# - 1 |
1494 |
p382 |
Mar 2016 |
Cunningham chain (16p + 15) |
| 5 | 5780736564512 · 3023# - 1 |
1301 |
p364 |
Mar 2015 |
Cunningham chain (16p + 15) |
| 6 | 1542946580224 · 2851# - 1 |
1231 |
p364 |
Aug 2023 |
Cunningham chain (16p + 15) |
| 7 | 744029027072 · 10111# - 1 |
4362 |
p364 |
Feb 2025 |
Cunningham chain (8p + 7) |
| 8 | 1268118079424 · 8501# - 1 |
3640 |
p434 |
Oct 2023 |
Cunningham chain (8p + 7) |
| 9 | 109766820328 · 7877# - 1 |
3385 |
p395 |
Nov 2016 |
Cunningham chain (8p + 7) |
| 10 | 231692481512 · 7517# - 1 |
3218 |
p395 |
Sep 2016 |
Cunningham chain (8p + 7) |
| 11 | 375967981369 · 6907# · 8 - 1 |
2972 |
p382 |
May 2017 |
Cunningham chain (8p + 7) |
| 12 | 1128330746865 · 266441 - 1 |
20013 |
p158 |
Feb 2020 |
Cunningham chain (4p + 3) |
| 13 | 1815615642825 · 244046 - 1 |
13272 |
p395 |
Nov 2016 |
Cunningham chain (4p + 3) |
| 14 | 778965587811 · 236627 - 1 |
11038 |
p395 |
Sep 2016 |
Cunningham chain (4p + 3) |
| 15 | 272879344275 · 236622 - 1 |
11036 |
p395 |
Aug 2016 |
Cunningham chain (4p + 3) |
| 16 | 333645655005 · 235549 - 1 |
10713 |
p364 |
Mar 2015 |
Cunningham chain (4p + 3) |
|
References
- Cunningham1907
- A. Cunnningham, "On hyper-even numbers and on Fermat's numbers," Proc. Lond. Math. Soc., series 2, 5 (1907) 237--274.
- Guy94 (SectionA7)
- R. K. Guy, Unsolved problems in number theory, Springer-Verlag, 1994. New York, NY, ISBN 0-387-94289-0. MR 96e:11002 [An excellent resource! Guy briefly describes many open questions, then provides numerous references. See his newer editions of this text.]
- Lehmer1965
- D. H. Lehmer, "On certain chains of primes," Proc. Lond. Math. Soc., series 3, 14a (1965) 183--186. MR 31:2222
- LM1980
- C. Lalout and J. Meeus, "Nearly-doubled primes," J. Recreational Math., 13 (1980-81) 30--35.
- Loh89
- G. Löh, "Long chains of nearly doubled primes," Math. Comp., 53 (1989) 751-759. MR 90e:11015 (Abstract available) [Chains of primes for which each is either twice the proceeding one plus one, or each is either twice the proceeding one minus one. See also [Guy94, section A7].]
- Ribenboim95 (p 333)
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- Yates82
- S. Yates, Repunits and repetends, Star Publishing Co., Inc., Boynton Beach, Florida, 1982. pp. vi+215, MR 83k:10014
Printed from the PrimePages <t5k.org> © Reginald McLean.