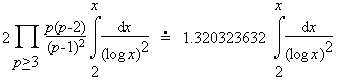twin prime conjecture
The (weak) twin prime conjecture is that there are infinitely many twin primes.
There is also a strong form of this conjecture [HL23] which states that there are about
twin primes less than or equal to x. The constant written above as an infinite product is the twin primes constant. See the page "a simple heuristic" linked below for information on how this conjecture is formed.
See Also: BrunsConstant, TwinPrimeConstant
Related pages (outside of this work)
- Twin primes (research and records)
- A simple heuristic (draft article about construcitng such conjectures)
References:
- HL23
- G. H. Hardy and J. E. Littlewood, "Some problems of `partitio numerorum' : III: on the expression of a number as a sum of primes," Acta Math., 44 (1923) 1-70. Reprinted in "Collected Papers of G. H. Hardy," Vol. I, pp. 561-630, Clarendon Press, Oxford, 1966.
Printed from the PrimePages <t5k.org> © Reginald McLean.