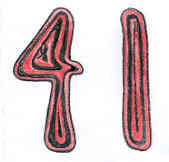
41

This number is a prime.

Just showing those entries submitted by 'Bergot': (Click here to show all)

The reversal of 41 is 14; add p^p, where p is prime to get the original prime (i.e., 14 + 3^3 = 41). Is there a larger prime with this property? [Bergot]

The product of the digits of 41 is 4, and the sum is 5; hence 4*41+5=169=13^2 and 41 is the 13th prime. Further, 5*41+4=209 and reversing the digits gives 902, add to 209 to get 1111, which is four one's or 41. [Bergot]

(There is one curio for this number that has not yet been approved by an editor.)