2657
This number is a prime.
 The American mathematician Lowell Schoenfeld (1920-2002)
proved that if the Riemann hypothesis was true, then
The American mathematician Lowell Schoenfeld (1920-2002)
proved that if the Riemann hypothesis was true, then
for all x greater than or equal to 2657.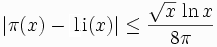
 The start of a run of 14 consecutive 4-digit prime numbers
separated by one-digit prime gaps. [Nie]
The start of a run of 14 consecutive 4-digit prime numbers
separated by one-digit prime gaps. [Nie]
 2657# + 1 is the smallest titanic primorial prime of form p# + 1. [Loungrides]
2657# + 1 is the smallest titanic primorial prime of form p# + 1. [Loungrides]
 2657 has a peculiar property. It can be written as the sum of a power of its first digit and a power of its last digit,
i.e., 2657 = 2^8 + 7^4. [Leonardis]
2657 has a peculiar property. It can be written as the sum of a power of its first digit and a power of its last digit,
i.e., 2657 = 2^8 + 7^4. [Leonardis]
 There are 2657 cases of a distinct-digit positive integer having a square that has exactly one odd digit. The largest has a beastly square. [Gaydos]
There are 2657 cases of a distinct-digit positive integer having a square that has exactly one odd digit. The largest has a beastly square. [Gaydos]
 2657 is the 4-digit prime number p with the most primes
from p to p+100. There are 19 primes from 2657 to 2757
(2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693,
2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749,
2753). [Jacobs]
2657 is the 4-digit prime number p with the most primes
from p to p+100. There are 19 primes from 2657 to 2757
(2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693,
2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749,
2753). [Jacobs]