Heuristics Model for the Distribution of Mersennes

Let M_n be the nth Mersenne prime.  Take a careful look at the graph of log₂(log₂(M_n)) versus n.  (That is, the logarithm base two of the logarithm base two of the nth Mersenne.)

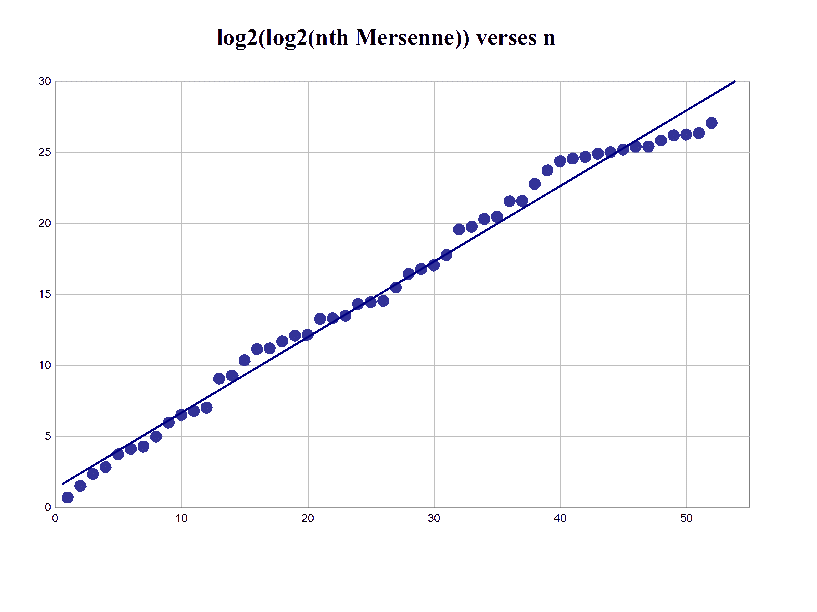
One can not miss that this graph is amazingly linear(at least until the las dozen).  Erhardt (and many others after him) looked at the limited data and guessed that the geometric mean of the ratio of two successive Mersenne exponents 3/2.

Some time later Pomerance and Lenstra each (independently) [Pomerance81, p. 101] suggested this should be 2 raised to 1/e^gamma or about 1.47576, not 3/2, where gamma is Euler's constant gamma.  This is now the accepted value, but why?  Below we will answer this question using a simple heuristic argument.  This means we try to make it seem plausible (and eventually hope for a proof someday).

If you are in a rush, then let me simply follow Ribenboim [Ribenboim95] and state the factor e^gamma comes by analogy from Mertens' theorem.  But if you have time, take a sip of coffee and join us for a little mathematics.

Heuristic Derivation of this Mersenne Conjecture

We will argue for Lenstra and Pomerance's conjecture in the form given in 1983 by Wagstaff [Wagstaff83] (though we do not follow his reasoning here):

1. The number of Mersenne primes less than or equal to x is about (e^gamma/log 2) * log log x.  (Here gamma is Euler's constant). 
2. The expected number of Mersenne primes 2^p-1 with p between x and 2x is about e^gamma.
3. The probability that  2^p-1 is prime is about (e^gamma log ap )/(p log 2) where a=2 if p=3 (mod 4), and a=6 if p=1 (mod 4).

So how might we reach this conclusions?  We will start by estimating the probability that 2^k-1 is prime, and then combine that guess with several others.

The probability that 2^k-1 is prime

As our first step in estimating the probability that 2^k-1 is prime, we recall that for 2^k-1 to be prime, k must be prime (proof).  Next, by prime number theorem the probability that a random positive integer k is prime is (asymptotic to) 1/log(k) (where log x is the natural logarithm).  For the next step we will assume this is the case: that k is prime.

Next, we might want to again use the prime number theorem to guess that the probability that 2^k-1 is prime, is 1/log(2^k-1), or about 1/(k log 2); but 2^k-1 does not behave like a "random number."  For example, 2^k-1 can only be divisible by primes of the form 2mk+1 for certain integers m (proof).  So we will need to adjust the estimate of probability we get from the prime number theorem as follows.

Since 2^k-1 can not be even--we multiply our estimate of the primality probability by 2 (since 2 divides 1/2 of the integers).  Similarly, unless k is 2, 2^k-1 can not be divisible by 3, so we multiply our estimate of the primality probability by 3/2=1/(1-1/3) (since 3 divides 1/3rd of the integers).  In fact, for each prime q less than 2k+1 we must multiply our estimate by q/(q-1) = 1/(1-1/q).  So we now guess that the probability that 2^k-1 is prime (for a given prime q) is about

where q is the largest prime less than 2k.  This product can be estimated using Mertens' theorem to be

where as above gamma is Euler's constant.

"But wait" you might say, "you have log(2k), but Wagstaff says log(ak) where a varies."  Then I'd be forced to admit I omitted something else we know about the divisors of Mersenne numbers: they are always congruent to +/-1 modulo 8.  When k is 3 modulo 4, this means m must be 0 or 3 modulo 4, so the smallest such prime is at least 6k+1 and we must replace the 2k in our argument above with 6k, just as Wagstaff says.  When k is 1 modulo 4, m may be 1, so we can stick with the 2k above in this case.  This completes the derivation of Wagstaff's third conclusion.

Toward a combined estimate

Let's go one step further and combine our two probability estimates: the probability k is prime and the probability the resulting 2^k-1 is prime.  We then get the probability that 2^k-1 is prime (for a random positive integer k) to be

(with a=2 or 6 as above).  For large k (and indeed the "average" integer is large), log(ak)=log a + log k is very close (asymptotically) to just log k, so our probability estimate simplifies to

Next we will use this heuristic estimate to derive the first of Wagstaff's three conclusions.

The number of Mersennes less than x

So, how many Mersenne primes 2^k-1 do we expect with 1 < k < n ?  We can find this by adding the probabilities for k=1, 2, 3, ... up to n.  The easiest way to approximate this sum would be to integrate.  This gives us

Now let's rephrase this.  If we wish to restrict the size of n so that 2^k-1 < x, then we must stop with n log 2 near log x, hence log n near log log x.  So we have

This is the first of Wagstaff's conclusions (from which the second follows trivially).

Note: The above is definitely not the argument you find in Wagstaff's article, but I think it is easier to follow and generalizes smoothly to many other forms.