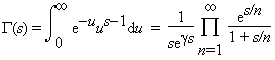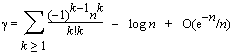Euler's constant
Euler's Constant (or Mascheroni's constant) is the limit (as n goes to infinity) of
1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n - log n.
This constant is often denoted by the lower-case Greek letter gamma γ and is approximately
0.57721566 4901532860 6065120900 8240243104 2159335939 9235988057 6723488486 7726777664 6709369470 6329174674 9514631447 2498070824 8096050401 4486542836 2241739976 4492353625 3500333742 9373377376 7394279259 5258247094 9160087352 0394816567 ...
Even though over 1,000,000 digits of this number have been calculated, it is not yet known if it is a rational number (the ratio of two integers a/b). But if it is rational, the denominator (b) must have more than 244,663 digits!
The constant gamma occurs in many places in number theory; we will give three examples. First, de la Vallée Poussin proved the following in 1898:
Take any positive integer n and divide it by each positive integer m less than n. Calculate the average (mean) fraction by which the quotient n/m falls short of the next integer. The larger n gets, the closer the average gets to γ (not 1/2!)
Second, the gamma function is defined as follows:
Third, it is conjectured that the number of Mersenne primes Mp less than x is about
Finally, it is possible to calculate Euler's constant from the nth harmonic number Hn, but a better approach is to use the following:
See Also: MertensTheorem
References:
- BM80
- Brent, R. P. and McMillan, E. M., "Some new algorithms for high-precision computation of Euler's constant," Math. Comp., 34:149 (1980) 305--312. MR 82g:10002
- Poussin1989
- C. de la Vallée Poussin, "Sur les valeurs moyennes de certaines fonctions arithmétiques," Annales de la société scientifique de Bruxelles, 22 (1898) 84--90.