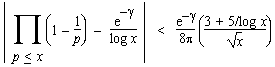Mertens' theorem

Mertens used Chebyshev's theorem (a weak version of the prime number theorem) to prove that

.

This is now called Mertens' Theorem.

Assuming the Riemann hypothesis, Schoenfeld showed that when x > 8, we have the following error bound

where γ is Euler's constant.

Related pages (outside of this work)

• Franz Mertens

References:

BS96 (p. 210,234)

E. Bach and J. Shallit, Algorithmic number theory, Foundations of Computing Vol, I: Efficient Algorithms, The MIT Press, Cambridge, MA, 1996.  pp. xvi+512, MR 97e:11157 (Annotation available)