Unique
The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page.
This page is about one of those forms.
 Definitions and Notes
Definitions and Notes
The reciprocal of every prime p (other than two and
five) has a period, that is the decimal expansion of
1/p repeats in blocks of some set length (see the
period of a decimal expansion). This is called the period of
the prime p. Samuel Yates defined a unique prime
(or unique period prime) to be a prime which has a
period that it shares with no other prime. For example: 3,
11, 37, and 101 are the only primes with periods one, two,
three, and four respectively--so they are unique primes.
But 41 and 271 both have period five, 7 and 13 both have
period six, 239 and 4649 both have period seven, and each
of 353, 449, 641, 1409, and 69857 have period thirty-two,
showing that these primes are not unique primes.
As we would expect from any object labeled "unique," unique primes are extremely rare. For example, even though there are over 1047 primes below 1050, only eighteen of these primes are unique primes. We can find the unique primes using the following theorem.
- Theorem.
- The prime p is a unique prime of period n
if and only if
is a power of p where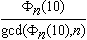
.gif) is the nth cyclotomic polynomial.
is the nth cyclotomic polynomial.
 Record Primes of this Type
Record Primes of this Type
rank prime digits who when comment 1 R(109297) 109297 E12 May 2025 Repunit, ECPP, unique 2 R(86453) 86453 E3 May 2023 Repunit, ECPP, unique 3 R(49081) 49081 c70 Mar 2022 Repunit, unique, ECPP 4 Phi(717, - 1072) 34273 E1 Aug 2025 Unique, ECPP 5 Phi(34051, - 10) 32033 E1 Aug 2025 Unique, ECPP 6 Phi(23023, - 100) 31681 E1 Aug 2025 Unique, ECPP 7 Phi(4613, - 100000000) 31585 E1 Aug 2025 Unique, ECPP 8 Phi(10295, - 10000) 31360 E1 Jul 2025 Unique, ECPP 9 Phi(11589, - 10000) 30897 E1 Oct 2022 Unique, ECPP 10 Phi(36547, - 10) 29832 E1 Jun 2022 Unique, ECPP 11 Phi(11867, - 100) 23732 c47 Dec 2021 Unique, ECPP 12 Phi(35421, - 10) 23613 c77 Jun 2021 Unique, ECPP 13 Phi(1203, 1027) 21600 c47 Nov 2021 Unique, ECPP 14 Phi(39855, - 10) 21248 c95 Nov 2020 Unique, ECPP 15 Phi(23749, - 10) 20160 c47 Apr 2014 Unique, ECPP 16 Phi(14943, - 100) 18688 c47 Mar 2014 Unique, ECPP 17 Phi(18827, 10) 18480 c47 May 2014 Unique, ECPP 18 Phi(26031, - 10) 17353 c47 Apr 2014 Unique, ECPP 19 Phi(2949, - 100000000) 15713 c47 May 2013 Unique, ECPP 20 Phi(5015, - 10000) 14848 c47 Apr 2013 Unique, ECPP
 References
References
- Caldwell97
- C. Caldwell, "Unique (period) primes and the factorization of cyclotomic polynomial minus one," Mathematica Japonica, 46:1 (1997) 189--195. MR 99b:11139 (Abstract available)
- CD1998
- C. Caldwell and H. Dubner, "Unique period primes," J. Recreational Math., 29:1 (1998) 43--48.
- Yates1980
- S. Yates, "Periods of unique primes," Math. Mag., 53:5 (1980) 314.
Printed from the PrimePages <t5k.org> © Reginald McLean.