Generalized Unique
The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page.
This page is about one of those forms.
 Definitions and Notes
Definitions and Notes
The reciprocal of every prime p (other than two and five) has a period, that is the decimal expansion of 1/p repeats in blocks of some set length (see the period of a decimal expansion). This is called the period of the prime p. Samuel Yates defined a unique prime (or unique period prime) to be a prime which has a period that it shares with no other prime. For example: 3, 11, 37, and 101 are the only primes with periods one, two, three, and four respectively--so they are unique primes. But 41 and 271 both have period five, 7 and 13 both have period six, 239 and 4649 both have period seven, and each of 353, 449, 641, 1409, and 69857 have period thirty-two, showing that these primes are not unique primes.
As we would expect from any object labeled "unique," unique primes are extremely rare. For example, even though there are over 1047 primes below 1050, only eighteen of these primes are unique primes. We can find the unique primes using the following theorem.
- Theorem.
- The prime p is a unique prime of period n
if and only if
is a power of p where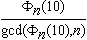
.gif) is the nth cyclotomic polynomial.
is the nth cyclotomic polynomial.
It is possible to generalize this to other bases: A prime p is a unique prime in base b, if and only if, for some integer n, it is the only prime divisor of Φn(b) which does not divide n (and it may occur as a prime power). For example, the Gaussian Mersenne norms (other than 5) all have the form
2n ± 2(n+1)/2 +1.Since Φ4(x) = x2+1, these can be written as Φ4(2(n+1)/2± 1)/2, showing these are all generalized unique primes.
 Record Primes of this Type
Record Primes of this Type
rank prime digits who when comment 1 5166932097152 - 5166931048576 + 1 11981518 L4561 Oct 2023 Generalized unique 2 4658592097152 - 4658591048576 + 1 11887192 L4561 May 2023 Generalized unique 3 1234471048576 - 123447524288 + 1 5338805 L4561 Feb 2017 Generalized unique 4 215317227 + 27658614 + 1 4610945 L5123 Jul 2020 Gaussian Mersenne norm 41?, generalized unique 5 143332786432 - 143332393216 + 1 4055114 L4506 Jan 2017 Generalized unique 6 3328218524288 - 3328218262144 + 1 3419518 p453 Dec 2025 Generalized unique 7 3268739524288 - 3268739262144 + 1 3415412 p453 Nov 2025 Generalized unique 8 2637072524288 - 2637072262144 + 1 3366518 p453 Dec 2025 Generalized unique 9 36608603 - 33304302 + 1 3153105 L5123 Jun 2023 Generalized unique 10 844833524288 - 844833262144 + 1 3107335 L4506 Jan 2017 Generalized unique 11 712012524288 - 712012262144 + 1 3068389 L4506 Jan 2017 Generalized unique 12 558640393216 - 558640196608 + 1 2259865 L4506 Jan 2017 Generalized unique 13 237804393216 - 237804196608 + 1 2114016 L4506 Jan 2017 Generalized unique 14 34043119 + 32021560 + 1 1929059 L5123 Jun 2023 Generalized unique 15 93606354294 + 93606177147 + 1 1761304 p437 Nov 2023 Generalized unique 16 55599354294 + 55599177147 + 1 1681149 p437 Nov 2023 Generalized unique 17 2533333262144 - 2533333131072 + 1 1678690 p453 Jan 2026 Generalized unique 18 2507493262144 - 2507493131072 + 1 1677523 p453 Nov 2025 Generalized unique 19 2044075262144 - 2044075131072 + 1 1654259 p453 Nov 2025 Generalized unique 20 1082083262144 - 1082083131072 + 1 1581846 L4506 Jan 2017 Generalized unique
 References
References
- Caldwell97
- C. Caldwell, "Unique (period) primes and the factorization of cyclotomic polynomial minus one," Mathematica Japonica, 46:1 (1997) 189--195. MR 99b:11139 (Abstract available)
- CD1998
- C. Caldwell and H. Dubner, "Unique period primes," J. Recreational Math., 29:1 (1998) 43--48.
- Yates1980
- S. Yates, "Periods of unique primes," Math. Mag., 53:5 (1980) 314.