Sophie Germain (p)
The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page.
This page is about one of those forms.
 Definitions and Notes
Definitions and Notes
If both p and 2p+1 are prime, then
p is a Sophie Germain prime.
The first few Sophie Germain primes are 2, 3, 5, 11,
23, 29, 41, 53, 83, 89, 113, and 131. Around 1825 Sophie
Germain proved that the first case of Fermat's Last
Theorem is true for such primes. Soon after Legendre
began to generalize this by showing the first case of
FLT also holds for odd primes p such that
kp+1 is prime, k=4, 8, 10, 14 and 16.
In 1991 Fee and Granville [FG91]
extended this to k<100, k not
a multiple of three. Many similar results were
also shown, but now that Fermat's Last Theorem
has been proven by Wiles, they are of less
interest.
Are there infinitely many Sophie Germain primes? Ribenboim indicates that the sieve methods of Brun (see the twin primes page) can be used to estimate that the number of primes p < x for which kp+a is prime is bounded above by C x/(log x)2 (so they have density zero among the primes). Heuristically, it seems reasonable to conjecture that there is a lower bound of this form as well. More specifically (see a simple heuristic), it is conjectured that the number of Sophie Germain primes less than N is asympototic to
where C2 is the twin prime constant (estimated by Wrench and others to be approximately 0.6601618158...). This estimate works suprisingly well! For example: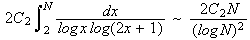
| N | actual | estimate |
|---|---|---|
| 1,000 | 37 | 39 |
| 100,000 | 1171 | 1166 |
| 10,000,000 | 56032 | 56128 |
| 100,000,000 | 423140 | 423295 |
| 1,000,000,000 | 3308859 | 3307888 |
| 10,000,000,000 | 26569515 | 26568824 |
Euler and Lagrange proved that if we also have p ≡ 3 (mod 4) and p > 3, then 2p+1 is prime (and p is a Sophie Germain prime) if and only if 2p+1 divides the Mersenne Mp.
(Thanks to Chip Kerchner for the last two entries in the table above.)
 Record Primes of this Type
Record Primes of this Type
rank prime digits who when comment 1 2618163402417 · 21290000 - 1 388342 L927 Feb 2016 Sophie Germain (p) 2 18543637900515 · 2666667 - 1 200701 L2429 Apr 2012 Sophie Germain (p) 3 47356235323005 · 2333443 - 1 100391 L6077 Oct 2024 Sophie Germain (p) 4 21480284945595 · 2333443 - 1 100390 L6029 May 2024 Sophie Germain (p) 5 66629493 · 2269334 - 1 81086 L3494 May 2025 Sophie Germain (p) 6 22942396995 · 2265776 - 1 80017 L3494 Nov 2023 Sophie Germain (p) 7 183027 · 2265440 - 1 79911 L983 Mar 2010 Sophie Germain (p) 8 648621027630345 · 2253824 - 1 76424 x24 Nov 2009 Sophie Germain (p) 9 620366307356565 · 2253824 - 1 76424 x24 Nov 2009 Sophie Germain (p) 10 10957126745325 · 2222333 - 1 66942 L5843 Nov 2023 Sophie Germain (p) 11 20690306380455 · 2222332 - 1 66942 L5843 Nov 2023 Sophie Germain (p) 12 10030004436315 · 2222333 - 1 66942 L5843 Nov 2023 Sophie Germain (p) 13 8964472847055 · 2222333 - 1 66942 L5843 Nov 2023 Sophie Germain (p) 14 1068669447 · 2211088 - 1 63553 L4166 May 2020 Sophie Germain (p) 15 99064503957 · 2200008 - 1 60220 L95 Apr 2016 Sophie Germain (p) 16 12443794755 · 2184516 - 1 55555 L3494 Sep 2021 Sophie Germain (p) 17 21749869755 · 2184515 - 1 55555 L3494 Sep 2021 Sophie Germain (p) 18 14901867165 · 2184515 - 1 55555 L3494 Sep 2021 Sophie Germain (p) 19 607095 · 2176311 - 1 53081 L983 Sep 2009 Sophie Germain (p) 20 48047305725 · 2172403 - 1 51910 L99 Jan 2007 Sophie Germain (p)
 Related Pages
Related Pages
- The World of mathematics': Sophie Germain Primes
- The Prime Glossary': Sophie Germain prime
- The chronology of prime number records' Sophie prime records by year
 References
References
- Agoh2000
- Agoh, Takashi, "On Sophie Germain primes," Tatra Mt. Math. Publ., 20 (2000) 65--73. Number theory (Liptovský Ján, 1999). MR 1845446
- CFJJK2006
- Csajbók, T., Farkas, G., Járai, A., Járai, Z. and Kasza, J., "Report on the largest known Sophie Germain and twin primes," Ann. Univ. Sci. Budapest. Sect. Comput., 26 (2006) 181--183. MR 2388687
- Dubner96
- H. Dubner, "Large Sophie Germain primes," Math. Comp., 65:213 (1996) 393--396. MR 96d:11008 (Abstract available)
- JR2007
- Jaroma, John H. and Reddy, Kamaliya N., "Classical and alternative approaches to the Mersenne and Fermat numbers," Amer. Math. Monthly, 114:8 (2007) 677--687. MR 2354438
- Peretti1987
- Peretti, A., "The quantity of Sophie Germain primes less than x," Bull. Number Theory Related Topics, 11:1-3 (1987) 81--92. MR 995537
- Ribenboim95
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- Yates1987
- Yates, Samuel, Sophie Germain primes. In "The mathematical heritage of C. F. Gauss," World Sci. Publ., River Edge, NJ, 1991. pp. 882--886, MR 1146271