strobogrammatic

Amateurs are often interested in numbers with special typographic qualities, such as the palindromes (which read the same forward and backward). A strobogrammatic integer (or strobogrammatic prime) is an integer (or respectively, a prime), which is the same number when rotated 180 degrees about an axis perpendicular to the plane on which the number is written, i.e., when turned upside down. E.g., 619. Invertible primes are those that yield a different prime when the prime is turned upside down. E.g., 109 becomes 601.

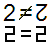Traditionally strobogrammatic and invertible integers (or primes) must contain only the digits 0, 1, 6, 8, or 9; but this definition depends not only on the base in which the number is written, but the set of glyphs with which the digits are represented. It could be that 2 and 5 rotate into themselves, or not.

Most mathematicians find this type of definition silly because it depends not only on the radix in which the number is written, but also on the glyphs/font used. But "silly" is a relative term. Consider the moral of the following incident related by Howard Eves (Return to Mathematical Circles 229o).

L. E. Dickson, during a discussion period that followed the presentation of a paper at a meeting of the American Mathematical Society, criticized the choice of the paper’s topic. "It is a lucky thing," he said, "that newspaper reporters do not attend these meetings. If they did, they would see how little our activities are related to the real needs of society." Fifteen minutes later he presented a paper of his own outlining a proof that every sufficiently large integer can be written as a sum of, not 1140 tenth powers (the best previous result), but 1046 tenth powers.

See Also: Palindrome, Tetradic, TriadicPrime

Related pages (outside of this work)

Printed from the PrimePages <t5k.org> © Reginald McLean.