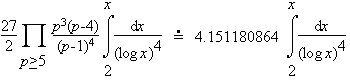quadruple

A prime quadruple is four consecutive primes, such that the first and the last differ by 8, that look like (p, p+2, p+6, p+8). For technical reasons (see prime k-tuple) the case (3, 5, 7, 11) is omitted. The first few are as follows.

(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), and (3461, 3463, 3467, 3469)

It is conjectured that there are infinitely many such primes. In fact the Hardy-Littlewood prime k-tuple conjecture suggests that the number less than x is approximately

The actual number less than 100,000,000 is 4768. The Hardy-Littlewood estimate above is 4734.

See Also: PrimeConstellation, Triple

Related pages (outside of this work)

• Prime k-tuplets (includes the largest known prime quadruples)

References:

HL23

G. H. Hardy and J. E. Littlewood, "Some problems of `partitio numerorum' : III: on the expression of a number as a sum of primes," Acta Math., 44 (1923) 1-70.  Reprinted in "Collected Papers of G. H. Hardy," Vol. I, pp. 561-630, Clarendon Press, Oxford, 1966.

Riesel94

H. Riesel, Prime numbers and computer methods for factorization, Progress in Mathematics Vol, 126, Birkhäuser Boston, Boston, MA, 1994.  ISBN 0-8176-3743-5. MR 95h:11142 [An excellent reference for those who want to start to program some of these algorithms. Code is provided in Pascal. Previous edition was vol. 57, 1985.]