greatest common divisor
The greatest common divisor (archaic: greatest common factor) of two integers a and b is the largest integer that divides them both. This is usually denoted by gcd(a,b), and sometimes by (a,b). For example, gcd(24,84)=12, gcd(-5,-100)=5, and gcd(46,111)=1. This is easily expanded to include any number of integers: gcd(27,30,36,81)=3.
Suppose the prime factorization of a is
![]() ,
and that of b is
,
and that of b is
![]() ,
then gcd(a,b) is
,
then gcd(a,b) is
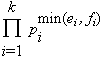 .
.
You might want to take the time to show the following:
- gcd(a,b) = gcd(b,a)
- gcd(a,b) = gcd(a,b+an) (for all integers n)
- There are integers n and m such that gcd(a,b) = an+bm
- gcd(a,b).lcm(a,b) = ab
This definition is often generalized in other situations. For example, the greatest common divisor of two polynomials with integer coefficients is the polynomial of highest degree (and largest leading coefficient) that divides them both.
See Also: EuclideanAlgorithm, LCM, RelativelyPrime
Related pages (outside of this work)