prime k-tuple conjecture
The prime k-tuple conjecture states that every admissible pattern for a prime constellation occurs infinitely often and that the number of occurrences of a prime constellation of length k is (infinitely often) greater than a constant times x/(log x)k.
Consider the cases k=2, 3, and 4. Here Hardy and Littlewood heuristically estimated the number of each pattern less than x is
| (k=2) | 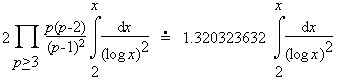 | ||
| (k=3) | 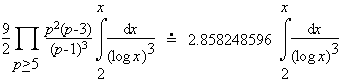 | ||
| (k=4) | 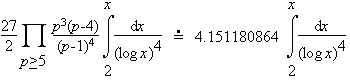 |
See Also: PrimeConstellation, PrimeNumberThm, DicksonsConjecture
Related pages (outside of this work)
References:
- Guy94 (A9)
- R. K. Guy, Unsolved problems in number theory, Springer-Verlag, 1994. New York, NY, ISBN 0-387-94289-0. MR 96e:11002 [An excellent resource! Guy briefly describes many open questions, then provides numerous references. See his newer editions of this text.]
- HL23
- G. H. Hardy and J. E. Littlewood, "Some problems of `partitio numerorum' : III: on the expression of a number as a sum of primes," Acta Math., 44 (1923) 1-70. Reprinted in "Collected Papers of G. H. Hardy," Vol. I, pp. 561-630, Clarendon Press, Oxford, 1966.
- Ribenboim95
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- Riesel94 (Chapter Three)
- H. Riesel, Prime numbers and computer methods for factorization, Progress in Mathematics Vol, 126, Birkhäuser Boston, Boston, MA, 1994. ISBN 0-8176-3743-5. MR 95h:11142 [An excellent reference for those who want to start to program some of these algorithms. Code is provided in Pascal. Previous edition was vol. 57, 1985.]
Printed from the PrimePages <t5k.org> © Reginald McLean.