Legendre symbol
Suppose p is an odd prime and a is any integer. The Legendre symbol (a|p) is defined to be
+1 if a is a quadratic residue (mod p), −1 if a is a quadratic non-residue (mod p) and, 0 if p divides a
Note: the Legendre symbol is often written vertically: ![]() .
.
Euler showed that (a|p) ≡ a(p−1)/2 (mod p). Using this we can show the following: Let p and q be odd primes, then
- (−1|p) = 1 if p ≡ 1 (mod 4), and (−1|p) = −1 if p ≡ 3 (mod 4);
- (a|p) (b|p) = (ab|p);
- if a ≡ b (mod p), then (a|p) = (b|p);
- (a2|p) = 1 unless p divides a.
For the prime 2 we have
- (2|p) = 1 if p ≡ 1 or 7 (mod 8), and
- (2|p) = −1 if p ≡ 3 or 5 (mod 8).
Far more difficult to prove is the quadratic reciprocity law:
- If p and q are distinct primes, then
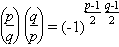 .
.
In other words, (p|q) = (q|p), unless p ≡ q ≡ 3 (mod 4), in which case (p|q) = −(q|p).
The Legendre symbol is often evaluated by using the Jacobi symbol.
See Also: JacobiSymbol
Printed from the PrimePages <t5k.org> © Reginald McLean.