elliptic curve primality proving
An Elliptic curve is a curve of genus one, that is a curve that can be written in the formE(a,b) : y2 = x3 + ax + b (with 4a3 + 27b2 not zero)
They are called "elliptic" because these equations first arose in the calculation of the arc-lengths of ellipses.
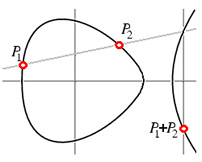 The
rational points on such a curve form a group with addition defined using the
"chord and tangent method:" That is, if the two points P1
and P2 are rational (have rational coefficients), then the line through
P1 and P2 intersects the curve again in a third rational
point which we call -(P1+P2) (the negative is to make
the associative law work out). Reflect through the x-axis to get
P1+P2. (If P1 and P2 are not
distinct, then use the tangent line at P1.)
The
rational points on such a curve form a group with addition defined using the
"chord and tangent method:" That is, if the two points P1
and P2 are rational (have rational coefficients), then the line through
P1 and P2 intersects the curve again in a third rational
point which we call -(P1+P2) (the negative is to make
the associative law work out). Reflect through the x-axis to get
P1+P2. (If P1 and P2 are not
distinct, then use the tangent line at P1.)
If we then reduce this group modulo a prime p we get a small group E(a,b)/p whose size can be used in roughly the way we use the size of (Z/pZ)* in the first of the classical primality tests. Let |E| be the order (size) of the group E:
Theorem: |E(a,b)/p| lies in the interval (p+1-2sqrt(p),p+1+2sqrt(p)) and the orders are fairly uniformly distributed (as we vary a and b).So the elliptic curve primality proving algorithm (ECPP for short) has replaced the groups of order n-1 and n+1 used in the classical test with a far larger range of group sizes. We can keep switching curves until we find one we can "factor". This improvement comes at the cost of having to do a great deal of work to find the actual size of these groups--but works for all numbers, not just those with very special forms.
About 1986 S. Goldwasser & J. Kilian [GK86] and A. O. L. Atkin [Atkin86] introduced elliptic curve primality proving methods. Atkin's method, ECPP, was implemented by a number of mathematicians, including Atkin & Morain [AM93].
Heuristically, ECPP is O((log n)5+eps) (with fast multiplication techniques) for some eps>0 [LL90]. It has been proven to be polynomial time for almost all choices of inputs. A version attributed to J. O. Shallit may be O((log n)4+eps).
François Morain, who first set the record for proving primality via ECPP, has made his program available to all. More recently Marcel Martin wrote a version called Primo for Windows machines. Version of these two programs hold most of the records.
Related pages (outside of this work)
- Top 20 ECPP primes
- Short introduction to ECPP
- A new record for ECPP by Francois Morain
References:
- AM93
- A. O. L. Atkin and F. Morain, "Elliptic curves and primality proving," Math. Comp., 61:203 (July 1993) 29--68. MR 93m:11136
- Atkin86
- A. O. L. Atkin, "Lecture notes of a conference," Boulder Colorado, (August 1986) Manuscript. [See also [AM93].]
- GK1999
- S. Goldwasser and J. Kilian, "Primality testing using elliptic curves," J. ACM, 46:4 (1999) 450--472. MR 2002e:11182
- GK86
- S. Goldwasser and J. Kilian, Almost all primes can be quickly certified. In "STOC'86, Proceedings of the 18th Annual ACM Symposium on the Theory of Computing (Berkeley, CA, 1986)," ACM, New York, NY, May 1986. pp. 316--329,
- LL90
- Lenstra, Jr., A. K. and Lenstra, Jr., H. W., Algorithms in number theory. In "Handbook of Theoretical Computer Science, Vol A: Algorithms and Complexity," The MIT Press, Amsterdam and New York, 1990. pp. 673-715, MR 1 127 178
- Morain98
- F. Morain, Primality proving using elliptic curves: an update. In "Algorithmic Number Theory, Third International Symposium, ANTS-III," J. P. Buhler editor, Lecture Notes in Comput. Sci. Vol, 1423, Springer-Verlag, June 1998. pp. 111--127, MR 2000i:11190