divisor
The divisors (or factors) of a positive integer are the integers that evenly divide it. For example, the divisors of 28 are 1, 2, 4, 7, 14 and 28. Of course 28 is also divisible by the negative of each of these, but by "divisors" we usually mean the positive divisors.The proper divisors of the integer n are the positive divisors of n other than n itself. The proper divisors of 27 are 1, 3 and 9.
Prime numbers are those integers greater than one whose only divisors are one and themselves (so whose only proper positive divisor is one).
Several number theoretic functions are related to the
divisors of n. For example, tau(n) (or
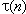 ) is the number of divisors of n, and
sigma(n) (or
) is the number of divisors of n, and
sigma(n) (or
.gif) )
is their sum.
)
is their sum.
There is another use of the word divisor: when we divide an integer a by a non-zero integer b, to get a quotient and remainder (see the division algorithm), b is the divisor and a is the dividend.
See Also: Divides, EulersPhi, AbundantNumber
Printed from the PrimePages <t5k.org> © Reginald McLean.