ON LUCAS'S TEST FOR THE PRIMALITY OF MERSENNE'S NUMBERS

D. H. L EHMER ¹.


    An examination of the literature on even perfect numbers since Euclid's time reveals only two contributions to the subject which are of genuine importance. The first of these is the celebrated theorem of Euler to the effect that every even perfect number is of Euclid's type 2 n-1 (2 n -1), where 2 n -1 is a prime. The second contribution is that of Lucas who gave a pair of theorems governing the primality of 2 4k ± 1 -1. A great deal of confusion exists in Lucas's writings about the exact enunciation and actual proofs of these tests for primality. Nevertheless, it is evident that Lucas was in possession of the facts needed to prove the sufficiency of his tests. The confusion arose from the fact that he was unable or unwilling to consider the necessity also.
    In 1930 the writer proved, as a by-product of an extended theory of Lucas's functions U n and V n , that the test which Lucas gave for 2 4k + 1 -1 is applicable also to 2 4k - 1 -1, and that his condition for primality is both necessary and sufficient. In fact the theorem may be stated as follows.

    THEOREM A.    The number N =  2 n -1, where n is an odd prime, is a prime if ,and only if, N divides the (n-1)-st term of the series,

S 1  = 4,   S 2  = 14,   S 3  = 194,   ...,   S k ,   ...,

where S k = S k 2 - 1 -2

    In 1932 Dr. A. E. Western ² gave a proof of this theorem by means of the theory of algebraic numbers. It is the purpose of this paper to give a very elementary yet self-contained proof of Theorem A.

    Notation and definitions. —Let

a = 1 + sqrt3,   b = 1 - sqrt3,
so that a + b = 2,   ab = -2,   a - b = 2 sqrt3.

We define two sequences of integers U r and V r by

U r = (a r - b r ) / (a - b),
V r = a r  + b r .

The following identities can be easily verified by using the above definitions.

(1) 2U r + s  = U r  V s  + V r  U s .
(2) (-2) s + 1  U r - s  = U s  V r  - U r  V s .
(3) 2V r + s  = V r  V s  + 12U r  U s .
(4) U 2r  = U r  V r .
(5) V 2r  = V r 2  + (-2) r + 1 .
(6) V r 2  - 12U r 2  = (-2) r + 2 .

    DEFINITION.    The rank of apparition of the odd prime p is the least positive subscript w (if it exists) for which Uw is divisible by p.

   In what follows p always represents a prime greater than 3. Before proving Theorem A it is convenient to establish three lemmas.

    LEMMA 1.    If w is the rank of apparition of p, then p divides U r if, and only if, w divides r.

    Proof.    Let S be the set of all subscripts r for which p divides U r . From (1) and (2) it follows that if r and s are members of S, so also are r ± s. Hence S coincides with the set of all integer multiples of its least positive member w. This proves Lemma 1.

    LEMMA 2.
(7) U p  congruent to (3/p)    (mod p).
(8) V p  congruent to 2          (mod p).

    Proof.    To prove (7) we expand U p as follows:

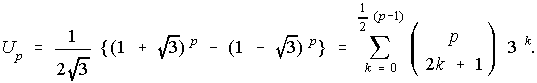Equation 1

All the binomial coefficients are divisible by p, except the last which is equal to unity. Hence

U p  congruent to 3 ½ (p - 1)  congruent to (3/p)    (mod p).

To prove (8) we expand V p in like manner, thus

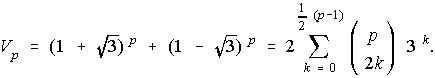Equation 2

In this case all the binomial coefficients except the first are divisible by p. Hence (8) follows at once.

    LEMMA 3.    If w is the rank of apparition of p, then w < p + 1.

    Proof.    It is obviously sufficient to prove that p divides U p + 1 U p - 1 . From (1) and (2) with r = p and s = 1 we have, since U 1  = 1 and V 1  = 2,

2U p + 1  = 2U p  + V p ,

-4U p - 1  = 2U p  - V p .

Using Lemma 2, we have

-8U p + 1 U p - 1  = 4U p 2  - V p 2 congruent to 4(±1) 2  - 4congruent to0     (mod p).

Hence Lemma 3 is proved.

    Proof of Theorem A.    We are now in a position to prove Theorem A without difficultly. The proof is in two parts.

    Proof of necessity.    Let N = 2 n -1 be a prime. We have to show that S n - 1 is divisible by N. Instead of the series S k we may consider the series

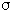8,  56,  3104,  ...,  Sigmak,  ...
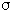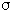in which Sigma k  = 2 2 k - 1 S k . Then it is sufficient to show that Sigma n - 1 is divisible by N. Since

S k + 1  = S k 2  - 2,
we have
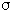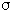Sigma k + 1  = Sigma k 2  - 2 2 k  + 1 .

Now if we put r = 2 k in (5) we get

V 2 k + 1  = (V 2 k ) 2  - 2 2 k  + 1 .

Moreover V 2  = 8 = Sigma 1 . Hence, in general,

Sigma k  = V 2 k .

We have to show then that V 2 n - 1  = V ½ (N + 1) is divisible by N. But from (5), with r = ½ (N + 1), we have

V N + 1  = V ½ 2 (N + 1)  - 4 · 2 ½ (N - 1) .

Hence it is sufficient to show that

(9) V N + 1  congruent to -4     (mod N),

since 2 is a quadratic residue of N = 8x - 1. But (9) follows from Lemma 2 and (3). In fact

2V N + 1  = V N  V 1  + 12U N  U 1  = 2V N  + 12U N .

To apply Lemma 2 with p = N, we note that N congruent to 1 (mod 3) and that

(3/N) = -(N/3) = -(1/3) = -1.

Hence we have

V N + 1  = V N  + 6U N  congruent to 2 - 6 congruent to -4    (mod N).

Hence (9) is established. This completes the proof of necessity.

    Proof of Sufficiency.    Let S n - 1 be divisible by N = 2 n  - 1. Then N divides

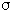Sigma n - 1  = 2 2 n - 2 S n - 1  = V 2 n - 1 .

Now let p be any prime factor of N and let w be the rank of apparition of p. Then p divides U 2 n since N divides U 2 n - 1 V 2 n - 1 , which is U 2 n by (4). By Lemma 1, w divides 2 n . On the other hand, w does not divide 2 n - 1 , for otherwise, by Lemma 1, p would divide U 2 n - 1 as well as V 2 n - 1 . This is impossible by (6) since p is odd. Hence w = 2 n . By Lemma 3,

p > w - 1 = 2 n  - 1 = N.

Hence p = N, so that N is a prime.

   In his paper Dr. Western gives a list of Mersenne numbers 2 n  - 1 examined by Lucas's tests. Since this list was made, Mr. R. E. Powers ³ has applied Theorem A to 2 241  - 1 and finds this number to be composite. This leaves the characters of 2 n  - 1 (for n < 257) undetermined for

n = 157, 167, 193, 199, 227, and 229.

Lehigh University,
          Bethlehem, Pa., U.S.A.

¹ Received 5 November, 1934; read 15 November, 1934.
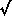² "On Lucas's and Pepin's tests for the primeness of Mersenne numbers", Journal London Math. Soc., 7 (1932), 130-137. This paper contains a list of references to papers on the subject.
³ Bull. Amer. Math. So., 40 (1934), 883.