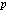- 1, in which p is a prime. This formula, first proposed
by Mersenne in 1644, does not yield a prime number for every
prime value given to p, but it has long been of interest
in studying primes and finding new ones.In 1611 Mersenne joined the Roman Catholic mendicant Order of Minims in Paris, and from 1614 to 1619, he taught philosophy at the Minim convent at Nevers. An ardent opponent of the mystical doctrines of alchemy, astrology, and related arcane arts, he vigorously supported science, defending the philosophy of René Descartes and the astronomical theories of Galileo. He held a post teaching philosophy at the convent L'Annonciade, Paris, and from 1620 he traveled extensively throughout western Europe.
The Mersenne numbers are generated from the formula 2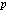
- 1, in which p is a prime. This formula, first proposed
by Mersenne in 1644, does not yield a prime number for every
prime value given to p, but it has long been of interest
in studying primes and finding new ones.
One of Mersenne's most important contributions was his long service as a communication link between philosophers and scientists throughout Europe. Because there were then no scientific journals, men might work a lifetime on the same project, never knowing of one another's existence. Mersenne met regularly and corresponded at length with eminent figures, including Descartes, Girard Desargues, Pierre de Fermat, Blaise Pascal, and Galileo, and it was said that "To inform Mersenne of a discovery, meant to publish it throughout the whole of Europe."
In addition to his work on prime numbers, Mersenne investigated cycloids (certain geometric curves) and proposed to the Dutch physicist Christiaan Huygens the use of the pendulum as a timing device, thus inspiring the pendulum clock. His published works include La Vérité dans les sciences (1625; "Truth in the Sciences") and Harmonie universelle (1636-37; "Universal Harmony").