Lehmer primitive part

The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page.

This page is about one of those forms.

Definitions and Notes

Lehmer defined a generalization of Lucas sequences as follows:

where a and b are the zeros of the polynomial z²-R^1/2z+Q for non-zero rational integers R, Q, and R-4Q.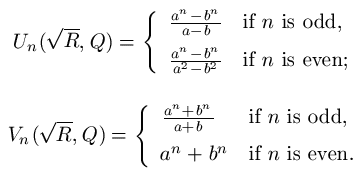 

A primitive divisor of a Lehmer is one that does not divide any previous term, and does not divide the product R(R-4Q).  Many of the references below (culminating in [BHV2002]) show that all but a finite number of the terms in a Lehmer sequence have primitive divisors.

If we let n=3^rm^s, where m > 3 is prime and min(r,s)>0. Then the numbers

(V(P,1,n/3)+1)/(V(P,1,n/(3m)+1)
(V(P,1,n/3)-1)/(V(P,1,n/(3m)-1)

are Lehmer primitive parts, with R=P+2 and Q=1, and their product is the Lucas primitive part primU(P,1,n).

Record Primes of this Type

rank prime digits who when comment 1 (V(6489, 1, 18903) - 1)/(V(6489, 1, 3) - 1) 72051 CH15 Sep 2025 Lehmer primitive part 2 (V(27730, 1, 16209) + 1)/(V(27730, 1, 9) + 1) 71976 CH15 Sep 2025 Lehmer primitive part 3 (V(10981, 1, 17553) + 1)/(V(10981, 1, 3) + 1) 70914 CH15 Aug 2025 Lehmer primitive part, cyclotomy 4 (V(8275, 1, 12447) - 1)/(V(8275, 1, 27) - 1) 48659 x45 Aug 2025 Lehmer primitive part 5 (V(24444, 1, 10809) + 1)/(V(24444, 1, 9) + 1) 47393 x45 Aug 2025 Lehmer primitive part 6 (V(60145, 1, 7317) - 1)/(V(60145, 1, 27) - 1) 34841 x45 Aug 2019 Lehmer primitive part 7 (V(28138, 1, 7587) - 1)/(V(28138, 1, 27) - 1) 33637 x45 Aug 2019 Lehmer primitive part 8 (V(48395, 1, 6921) - 1)/(V(48395, 1, 9) - 1) 32382 x45 Aug 2019 Lehmer primitive part 9 (V(77786, 1, 6453) + 1)/(V(77786, 1, 27) + 1) 31429 x25 Dec 2012 Lehmer primitive part 10 (V(73570, 1, 6309) - 1)/(V(73570, 1, 9) - 1) 30661 x25 Jun 2016 Lehmer primitive part 11 (V(28286, 1, 6309) + 1)/(V(28286, 1, 9) + 1) 28045 x25 Jun 2016 Lehmer primitive part 12 (V(59936, 1, 4863) + 1)/(V(59936, 1, 3) + 1) 23220 x25 Jan 2013 Lehmer primitive part 13 (V(45366, 1, 4857) + 1)/(V(45366, 1, 3) + 1) 22604 x25 Feb 2013 Lehmer primitive part 14 (V(23354, 1, 4869) - 1)/(V(23354, 1, 9) - 1) 21231 x25 Feb 2013 Lehmer primitive part 15 (V(428, 1, 8019) - 1)/(V(428, 1, 729) - 1) 19184 E1 Jun 2022 Lehmer primitive part, ECPP 16 (U(162, 1, 8581) + U(162, 1, 8580))/(U(162, 1, 66) + U(162, 1, 65)) 18814 E1 Jun 2022 Lehmer primitive part, ECPP 17 (U(859, 1, 6385) - U(859, 1, 6384))/(U(859, 1, 57) - U(859, 1, 56)) 18567 E1 Jun 2022 Lehmer primitive part, ECPP 18 (V(46662, 1, 3879) - 1)/(V(46662, 1, 9) - 1) 18069 x25 Dec 2012 Lehmer primitive part 19 (V(447, 1, 6723) + 1)/(V(447, 1, 81) + 1) 17604 E1 Jun 2022 Lehmer primitive part, ECPP 20 (V(561, 1, 6309) + 1)/(V(561, 1, 9) + 1) 17319 x25 May 2016 Lehmer primitive part

References

BHV2002

Bilu, Yu., Hanrot, G. and Voutier, P. M., "Existence of primitive divisors of Lucas and Lehmer numbers," J. Reine Angew. Math., 539 (2001) 75--122.  With an appendix by M. Mignotte.  MR1863855 (Annotation available)

Schinzel1963

Schinzel, A., "On primitive prime factors of Lehmer numbers. II," Acta. Arith., 8 (1962/1963) 251--257.  MR 27:1409

Schinzel1968

Schinzel, A., "On primitive prime factors of Lehmer numbers. III," Acta Arith., 15 (1968) 49--70.  MR0232744

Schinzel1970

Schinzel, A., "Corrigendum to the papers "On two theorems of Gelfond and some of their applications" and "On primitive prime factors of Lehmer numbers. III"," Acta Arith., 16 (1969/1970) 101.  MR0246840

Stewart1976

Stewart, C. L., Primitive divisors of Lucas and Lehmer numbers.  In "Transcendence theory: advances and applications (Proc. Conf., Univ. Cambridge, Cambridge, 1976)," Academic Press, 1977.  London, pp. 79--92, MR0476628

Stewart1977b

Stewart, C. L., Primitive divisors of Lucas and Lehmer numbers.  In "Transcendence theory: advances and applications (Proc. Conf., Univ. Cambridge, Cambridge, 1976)," Academic Press, 1977.  London, pp. 79--92, MR 57:16187

Stewart1983

Stewart, C. L., "On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers. III," J. London Math. Soc. (2), 28:2 (1983) 211--217.  MR 85g:11021

Voutier1995

Voutier, P. M., "Primitive divisors of Lucas and Lehmer sequences," Math. Comp., 64:210 (1995) 869--888.  MR1284673 (Annotation available)

Voutier1996

Voutier, P. M., "Primitive divisors of Lucas and Lehmer sequences. II," J. Th\'eor. Nombres Bordeaux, 8:2 (1996) 251--274.  MR1438469

Voutier1998

Voutier, P. M., "Primitive divisors of Lucas and Lehmer sequences. III," Math. Proc. Cambridge Philos. Soc., 123:3 (1998) 407--419.  MR1607969 [From the review: "The main result of this paper is that for any integer n>30 030, the nth element of any Lucas or Lehmer sequence has a primitive divisor."]